理詰めで音を作るのが難しいという話。
2オペレータ・フィードバックなしの簡単な例で。\(\)
詳細は「位相変調 フーリエ変換」とかでググってもらうとして、
モジュレータとキャリアの Multipleをそれぞれ \(M, C\) とすると、\(C\) 倍音が出るのは当然※として \(C+nM\) 倍音(\(n\) は整数)も出てくる(らしい)。
\(M=2,\ C=1\) なら、
| \(n\) | \(C+nM\ (M=2,\ C=1)\) | 倍音 |
|---|---|---|
| \(\vdots\) | \(\vdots\) | \(\vdots\) |
| \(n=-2\) | \(1-2\times 2=-3\) | 3倍音 |
| \(n=-1\) | \(1-1\times 2=-1\) | 1倍音 |
| \(n=0\) | \(1+0\times 2=1\) | 1倍音 |
| \(n=1\) | \(1+1\times 2=3\) | 3倍音 |
| \(n=2\) | \(1+2\times 2=5\) | 5倍音 |
| \(\vdots\) | \(\vdots\) | \(\vdots\) |
と、\(n\) がいくつでも奇数になる(つまり奇数倍音しか出ない)ので、矩形波っぽい音になるとか。
同じ要領で、\(M=1\) とか \(M=3\) とかは、いろんな整数倍音が(奇数も偶数も)出るので、鋸(のこぎり)波っぽい音になるとか。
ここまでは簡単なのだけれど、「じゃあ、それぞれの倍音の大きさはどうやって変えるの?」という話になる。
そうすると、第1種ベッセル関数というのが出てくる。なんだそれ。
Wikipedia にもあるけれど、もうちょい範囲を広げてグラフを書くと、こんな感じ。
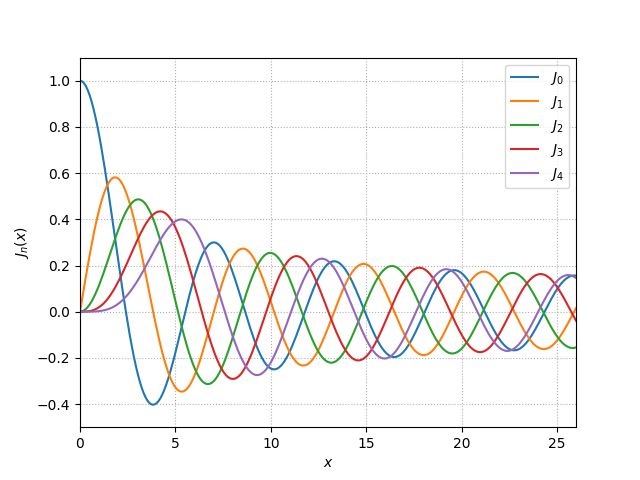
横軸の \(x\) が変調度、たくさんある \(J_n\) の \(n\) が上で書いた \(n\) と同じで、縦軸がそれぞれの倍音の大きさ。 \(M=2,\ C=1\) でいうと、\(J_0\) が1倍音・\(J_1\) が3倍音・…といった具合。
\(J_5\) 以降とか、あるいは負の方もあるけれど、グラフがごちゃごちゃになるので端折ってある。
で、「変調度 \(x\) って何だよ?」ということになるんだけれど、OPNとかならモジュレータの Total Level \((TL)\) から、だいたいこんな式で換算できる(はず)。
\[x=8\pi \times 2^{-\frac{TL}{8}}\]
それで、この \(TL\) を横軸にしてやると、
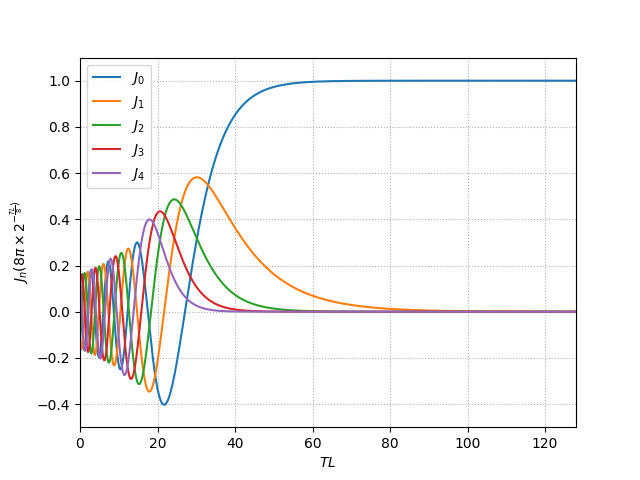
大きい方(変調しない方)から \(TL=40\) くらいまでは \(J_0\) つまり \(C\)倍音(キャリアの Multiple)が強く出ていて、ちょっとずつ \(n=1, 2, \ldots\) の順に増えていく感じなのだけれど、途中から倍音の方が強くなったり、\(TL=27\) 付近で \(C\)倍音 がなくなったりもする。
※ まったく「当然」ではなかった。
左の方がごちゃっとしてるので拡大すると、
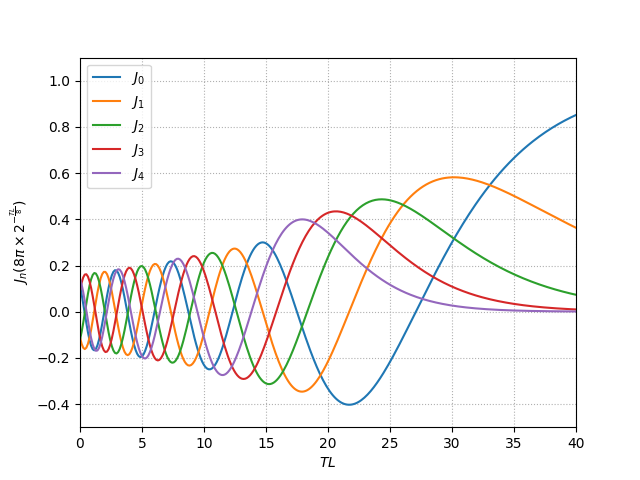
……拡大してもごちゃっとしている。この中で、作りたい音と同じ倍音比率になる値を探せと言われても困るわけです。あと、\(J_5\) 以降も少し書き足してやると、
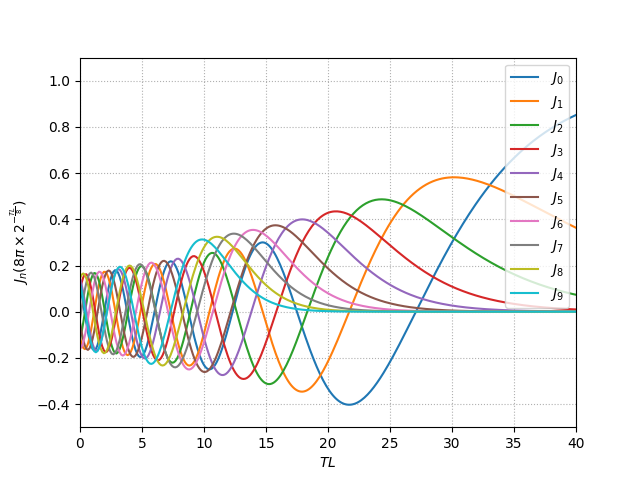
困るというか、そもそもほとんどの場合、狙ったような都合のいい倍音成分になる箇所なんてなくて「解なし」になるわけです。そりゃ2オペレータなので。
そんなわけで、3オペレータ・4オペレータ・フィードバックなどなどの出番になるのだけれど、2オペレータだけでもこれだけ複雑なのが、もっと複雑になるわけです。
詳しく書かなかったけれど、同じ倍音が複数出てきたときに強め合うか打ち消し合うか(縦軸の正負とか倍率の正負とか)の話とか、\(TL\) が整数でしか指定できない話とか、更にいろいろ絡みあって、自動で算出するにしても「この式に値を入れれば求められる!」みたいなのはたぶん無理で、近い結果になる組み合わせを探索する感じになるかと。
最近やってた「WSGっぽい音」は音色の時間変化がない(倍音構成も比較的簡単にわかる)ので自動化できないかと思ったけど、結局は大雑把にあたりをつけて「耳で聞いて調整」みたいな感じになってます。まあ、いまどきだと「ニューラルネットワークで一発!」とかできそうな気もするので、時間があったらやってみたい(誰かやって)。
