「FM音源と言いつつFM (Frequency Modulation) ではなくPM (Phase Modulation) だ!」という指摘がよくありますが、これは半分正しくて半分正しくない。
\(\)以下、「\(x(t)\) で周波数変調するのと \(\int x(t) dt\) で位相変調するのは同じこと」でわかる人には読む価値ないです。
(長くなるので厳密な話は端折ってます。)
角周波数 \(\omega\) のサイン波 \(y_1(t)\) は\[y_1(t)=\sin(\omega t)\] と表せるので、時間で周波数が変化する場合も同じようにして、角周波数 \(\omega+x(t)\) のサイン波 \(y_2(t)\) を \[y_2^?(t)=\sin\left((\omega+x(t))t\right)\] と書きたくなる(書いているものがある)けれども、これは正しくない(※)。
\(\sin\) 関数に与えるのは位相だけれども、(角)周波数は位相の変化の速さなので、位相を微分したものが角周波数、角周波数を積分したものが位相という関係。なので、単に \(t\) をかけるのではなくて、\[y_2(t)=\sin\left(\int (\omega+x(t)) dt\right)=\sin\left(\omega t + \int x(t) dt\right)\] で、これが正しく周波数変調 (FM) を表す式です。
具体的な関数を積分すると積分定数が出てきますが、\(t=0\) の時の位相は本題にあまり関係がないので、ここでは話を単純にするために 0 ということにして省略します。あと、教科書とかだと \(\sin\) じゃなくて \(\cos\) で書いてあったりしますが、同じような理由でどちらでもいいです。
とにかく積分なので、定数のときは \(t\) をかけるだけで良いけれども、それ以外のときは違うということですね。
あと、「ヤマハのFM音源のデータシートには位相変調の式が書いてあるけれど、FM音源の発明者であるチョウニング博士の本にはない」という話を見かけたのですが(そのデータシートや本は未確認)、少なくともチョウニング博士の1973年の論文にはこういう式があります。(変数の定義とかは論文の方を見てね。)\[e=A \sin(\alpha t + I \sin \beta t)\]
- John M. Chowning: “The Synthesis of Complex Audio Spectra by Means of Frequency Modulation”, Journal of the Audio Engineering Society, 21(7), 526–534, 1973.
これは(この式だけ見れば)位相変調ですので、ヤマハが独自に位相変調にしてしまったとかではないと思います。
それで、この場合の角周波数がどのように変化しているかですが、最初の \(\sin\) の中を微分すると、\[(\alpha t + I \sin \beta t)’ = \alpha + I\beta \cos \beta t\] となります。(位相を微分したので、これが角周波数です。)
つまり、\(I \sin \beta t\) で位相変調 (PM) しているということは、見方を変えれば \(I\beta \cos \beta t\) で周波数変調 (FM) しているとも言えるわけです。
最初の「正しくFM」と書いた式に当てはめるなら、\(e=A y_2(t),\ \ \omega = \alpha,\ \ x(t) =I\beta \cos \beta t\) で、\[e = A y_2(t) = A\sin\left(\alpha t + \int I\beta \cos \beta t dt\right) = A\sin\left(\alpha t + I \sin \beta t\right)\] が成り立っています。(積分定数は上記理由で省略)
それで、書かなかった \(I\) の定義ですが、\(I=d/m\) ……最大周波数偏移 \(d\) を変調波の周波数 \(m\) で割ったものとなっていて、\(m\) と \(\beta\) は周波数か角周波数かの違いでたぶん \(\beta=2\pi m\) なので、\(I\beta=2\pi d\) ですね。\(2\pi d \cos \beta t\) で周波数変調したのを、\(I\) という変数を置くことで位相変調のように書いただけとも言えます。
まとめると、「FM音源と言いつつ実装はPM」というのは正しいけれど、「FM音源と言いつつFMではない」というのは正しくない、ということになります。
おしまい。
※おまけ
FM音源の話からは逸れますが、仮に \(t=a\)[秒]時点での(瞬時)周波数が \(a\) Hz になるような変化を考えると、\(\omega = 0,\ \ x(t) = 2\pi t\) ですが、正しくない方の式に当てはめた場合 \[y_2^?(t) = \sin\left((\omega+x(t))t\right) = \sin(2 \pi t^2)\] で、こんなグラフになります。
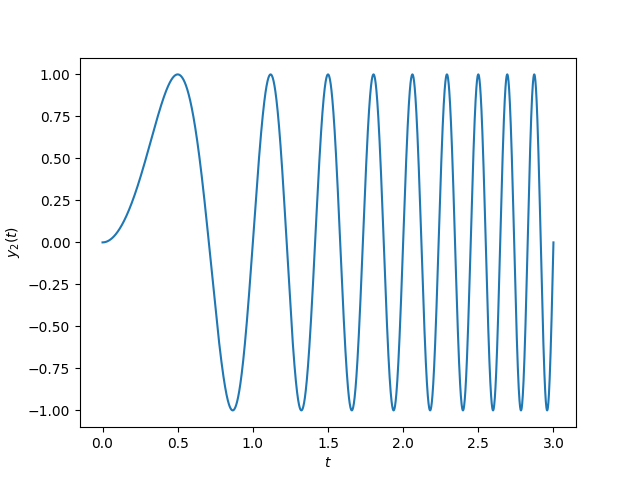
これだと、例えば \(t=1\) と \(2\) の間の1秒間で3回振動しているので、どう見ても想定より周波数が高いですよね。あえてこの式を解釈すると「\(t=0\) から \(a\) までの平均周波数が \(a\) Hz」でしょうか。当然、最初に想定したものとは違う周波数になってしまいます。
正しくは、\[y_2(t) = \sin\left(\int (\omega+x(t)) dt\right) = \sin\left(\int 2\pi t dt\right) = \sin(\pi t^2) \] です。(積分定数はry)
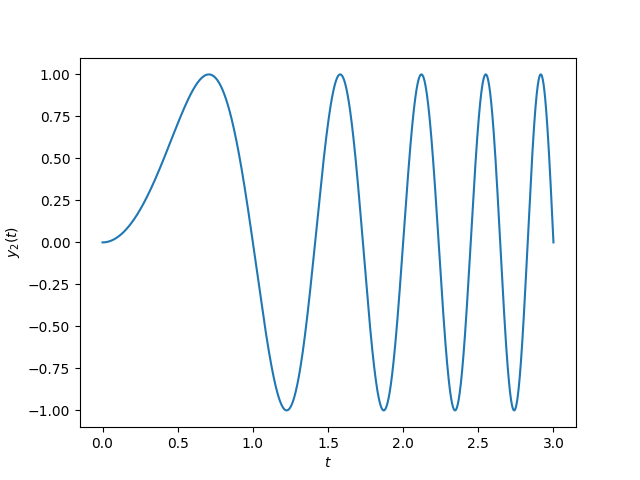
自前でスイープ信号を作ろうとしたときに「\(\sin(2\pi f t)\) の \(f\) と \(t\) を変化させながら値を取り出す」みたいなコードを書いてハマっているのを割と良く見ますが(自分もやったという意味で)、ダメなのは同じ理由です。普通のスイープ信号の周波数は何かの \(t\) 乗とかにすると思いますが、注意すべき点は同じです。
大抵の用途であれば、f を変化させながら、
x += 2.0 * PI * f * delta_t(delta_t は前回からの経過時間というか、サンプリングレートの逆数というか。)
みたいに位相 x を加算しながら \(\sin(x)\) を取り出すのが良いかと。(積分の近似ですね。)