前回の話でいうところの 3. の4ビットカウンタから先は大雑把に書くとこんな回路。
\(\)VOL 1 とか 2 とかあるスイッチの実体は CD4066。ソフトウェアでオンオフできる模様。
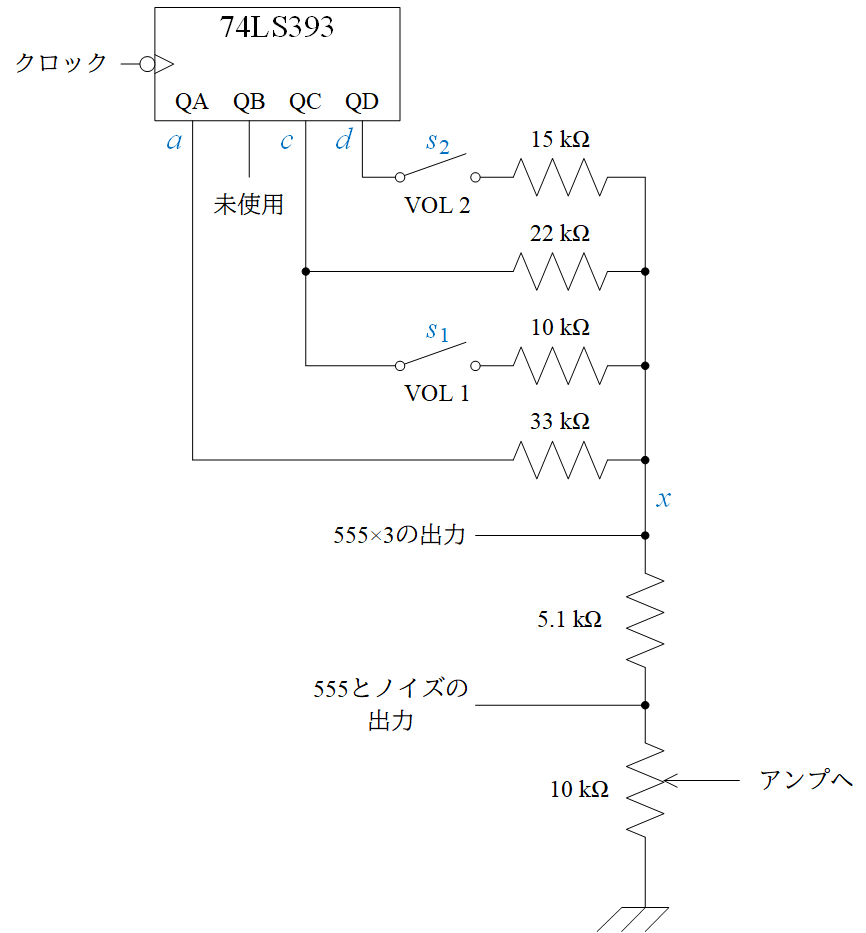
これで、アンプへの出力がどうなるかなのだけれど、他の555とかの出力を無視すれば、回路図中の \(x\) に比例するだろうからそれを求める。5.1kΩの 0.1 とか 4066 の内部抵抗とかも無視して、大雑把にオームの法則から電流を考えると、こんな式が成り立つはず。
\(a, c, d, x\) は回路図中の青字の部分の電圧、\(s_{1}, s_{2}\) はスイッチの状態 \(\{0, 1\}\)。
\[\frac{x}{5+10}=\frac{(d-x)s_2}{15}+\frac{(c-x)}{22}+\frac{(c-x)s_1}{10}+\frac{(a-x)}{33}\]
これを \(x\) について解くと、
\[x=\frac{22ds_{2}+33cs_{1}+15c+10a}{22s_{2}+33s_{1}+47}\]
(あってるかな?)
まとめるとこんな値になる。\(a, c, d\) は本当は0V・5Vだろうけれど、割合が見たいだけなので0, 1で。
| QD \(d\) | QC \(c\) | QB NC | QA \(a\) | \(s_{2}, s_{1}\) 0, 0 | \(s_{2}, s_{1}\) 0, 1 | \(s_{2}, s_{1}\) 1, 0 | \(s_{2}, s_{1}\) 1, 1 |
| 0 | 0 | 0 | 0 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0 | 0 | 0 | 1 | 0.213 | 0.125 | 0.145 | 0.098 |
| 0 | 0 | 1 | 0 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0 | 0 | 1 | 1 | 0.213 | 0.125 | 0.145 | 0.098 |
| 0 | 1 | 0 | 0 | 0.319 | 0.600 | 0.217 | 0.471 |
| 0 | 1 | 0 | 1 | 0.532 | 0.725 | 0.362 | 0.569 |
| 0 | 1 | 1 | 0 | 0.319 | 0.600 | 0.217 | 0.471 |
| 0 | 1 | 1 | 1 | 0.532 | 0.725 | 0.362 | 0.569 |
| 1 | 0 | 0 | 0 | 0.000 | 0.000 | 0.319 | 0.216 |
| 1 | 0 | 0 | 1 | 0.213 | 0.125 | 0.464 | 0.314 |
| 1 | 0 | 1 | 0 | 0.000 | 0.000 | 0.319 | 0.216 |
| 1 | 0 | 1 | 1 | 0.213 | 0.125 | 0.464 | 0.314 |
| 1 | 1 | 0 | 0 | 0.319 | 0.600 | 0.536 | 0.686 |
| 1 | 1 | 0 | 1 | 0.532 | 0.725 | 0.681 | 0.784 |
| 1 | 1 | 1 | 0 | 0.319 | 0.600 | 0.536 | 0.686 |
| 1 | 1 | 1 | 1 | 0.532 | 0.725 | 0.681 | 0.784 |
このうち、 \(s_{2}, s_{1}\) が1, 0のときをグラフにすると、
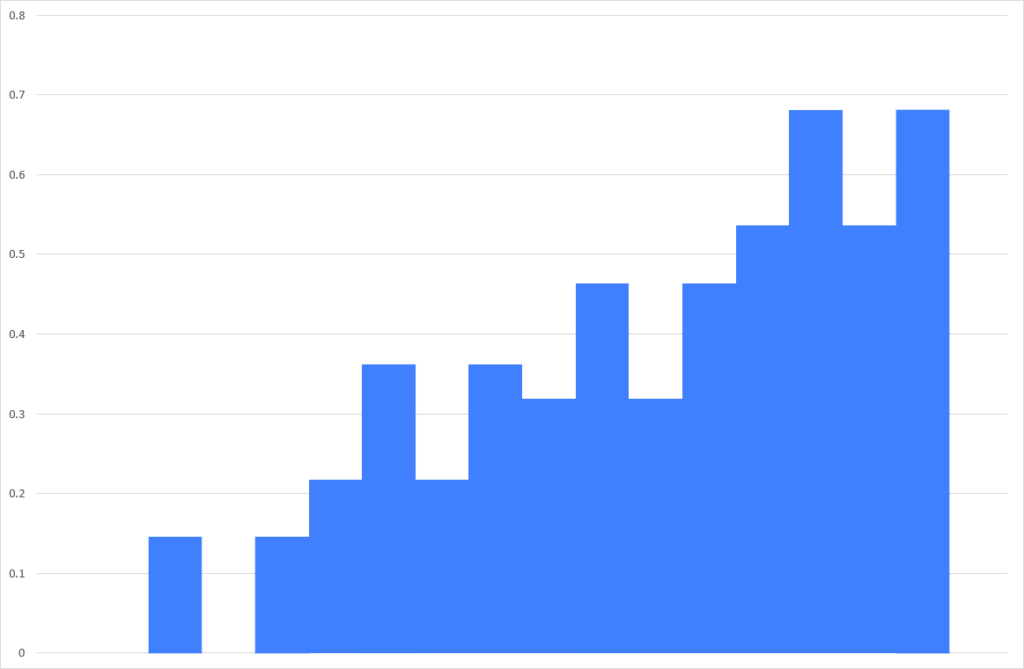
こんな感じだけれど、適当にみつけたアーケードのギャラクシアンのオープニング音(本物かどうかは不明)の波形(一部)が、
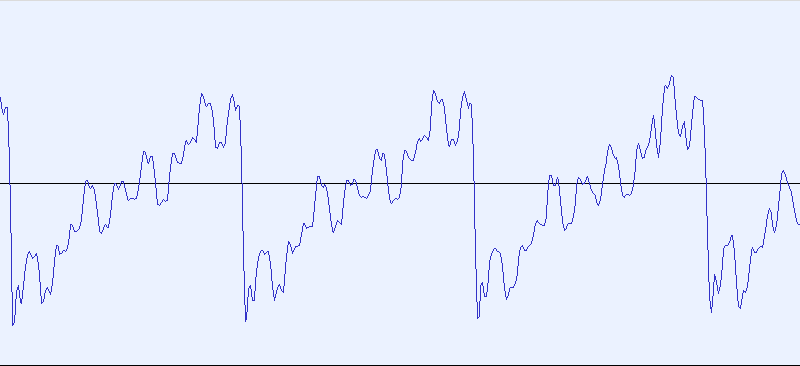
なので、だいたい合ってるように見える。
つづく(かもしれない)